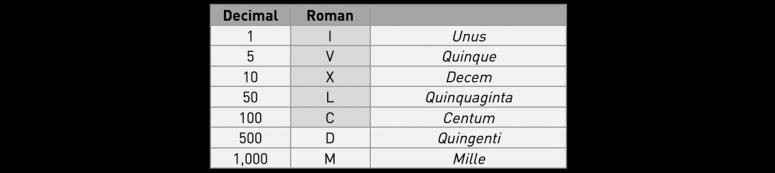
Roman numbers
The Romans did not know about zero, so there is no symbol in its numbering system to represent it. The Roman system employed a closed list of seven symbols to represent the basic numbers which combined together following certain rules on repetition, to allow every number to be obtained. It was a non-positional system, a system in which the symbols had intrinsic value independent of where they fell in the representation of the number.
Originally, Roman numerals were not actually uppercase symbols but born of the notches or marks that were cut in sticks and bones for counts (the Etruscans used I, Λ, X, ⋔, 8 and ⊕ to represent what Roman symbolized I, V, X, L, C and M). When the accounts were transferred to writing, some brands were easily identified with existing Roman letters.
Thus, the numeral I does not come from the letter I but from a carved notch in the rod. Every fifth notch was a double mark (⋀, ⋁, ⋋, ⋌) and every tenth notch was an X mark. Over time, the succession of marks (IIII Λ Λ IIII IIII IIII X X ...) gave rise to a system of symbols:
- 8 on a rod of accounts were eight units (Λ IIII III) that could shorten (ΛIII or VIII), since the existence of Λ implied above four notches.
- 18 was the eighth notch after the first ten, which could be abbreviated to X, and so the complete number was XΛIII (XVIII).
- Similarly, the number 4 in the rod was the mark I placed just before cutting Λ (V), so it could be written IIII or IΛ (IV).
The tenth V or X on the rod received an extra stroke:
- 50 was written in different ways (N, И, K), but perhaps the most common was an arrow pointed down as V with I located at the top (ↆ). In its evolution, this symbol was flattened to form an inverted T (⊥) and, shortly thereafter, would be identified with the letter L, which it resembled graphically
-
100 was also represented in different ways until it became its customary Ж form (X with I superimposed): it was written >I< or ƆIC after Ɔ or C was shortened and the variant C was the one that was imposed because, as a letter, it represented an abbreviation of one hundred (centum).
- 500 was like a Ɔ superimposed on a ⋌ or ⊢, becoming D or Ð. Using D identified with the value 500, as the graphic symbol Φ was the representation of half a thousand.
- 1000 was identified with the letter X enclosed in a circle or square (Ⓧ, ⊗, ⊕), or as Ψ, ↀ or after the Greek letter Φ (phi). The ↀ symbol evolved into CIƆ, ∞y ⋈ finally switching to M under the influence of the Latin word mille.
- Each M symbol added a thousand until a maximum of three (MMM). For numbers higher than 3,999, a horizontal line above the number was used to indicate that you had to understand to multiply by 1,000
- envolving the letter with symbol Π, was used to indicate that you had to understand to multiply by 100,000.
Rules
- The symbols are read from left to right, from highest to lowest value.
- If another numeral of equal or lesser value is written to the right of a Roman numeral, the value of it is added to the previous one (LXVII = 67).
- If a symbol is to the immediate left of another of higher value, it is subtracted from the first value according to the following:
- symbol I can only be subtracted from V and X.
- the X symbol can only be subtracted from L and C.
- the symbol C can only be subtracted from D and M.
- The symbol V is always added and can’t be put to the left of a numeral of greater value.
- Repeating V is not allowed, since the double is X.
- Repeating L is not allowed, since the double is C.
- Repeating D is not allowed, since the double is M.
- If I, X or C symbol appear in subtracting, they can only appear on the right of a unique symbol of higher value.
- If they appear between any two other minor figures, this value must be subtracted from the next value.
- If a symbol I, X or C appears in subtracting and is also repeated, its repetition must be located on the right side of the symbol that the subtraction occurs from (XCIX = 99).
- Two different symbols may appear in subtracting if they are not adjacent (CMXCIX = 999).
- To write numbers greater than 3,999, the value is understood to be multiplied by one thousand (1,000) by putting a horizontal line above it; if envolving the letter with symbol Π, the value should be multiplied by 100,000; if two lines appear, it means the value should be multiplied by one million (1,000,000).
- A maximum of three consecutive repetitions of the same symbol is allowed, although in antiquity I or X sometimes appear 4 times in a row.
Fractions
Although the Romans used a decimal system for integers, for fractions they used a duodecimal system (uncia), allowing them to handle common fractions (1/3, 1/4) more easily than a system based on tenths.
In currencies, many of which had values that were duodecimal fractions of the As coin as a unit of account, they used a notation system based on twelfths and halves. A dot (•) indicates a twelfth of the unit (uncia), and two, three, four and five points were used to represent fractions up to five twelfths. Six twelfths (half) are abbreviated with the letter S (semis), while points were also added to the fractions from seven to eleven twelfth parts. Each of these fractions had a name, which was also the name of the relevant currency (cf. Roman coinage).
Arithmetic operations: addition and subtraction
Complex operations were performed in a succession of different steps: first positional data was decoded into single notation, after which the numerals were rearranged from highest to lowest with the two addends maintaining their respective orders. With the subtractive notation removed, all the symbols are reordered and grouped, before the subtractive notation is reintroduced and the general rules of Roman numerals are applied.